Inteligência Artificial

Mineração de Dados com K-Means em Python: Um Guia Passo a Passo

Márcio Silva

Márcio Silva

— 3 min read
Mineração de Dados com K-Means em Python: Um Guia Passo a Passo

A mineração de dados é essencial para extrair insights valiosos de grandes volumes de informações. Um dos algoritmos mais populares para agrupamento é o K-Means. Neste tutorial, você aprenderá a aplicar o K-Means para segmentação de dados usando Python.

📌 Pré-requisitos

Antes de começar, certifique-se de ter as bibliotecas necessárias instaladas. Se ainda não as tiver, instale com o comando:

pip install numpy pandas matplotlib seaborn scikit-learn

🔹 1. Importando as Bibliotecas

Vamos começar importando as bibliotecas essenciais para o nosso exemplo:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.cluster import KMeans
from sklearn.preprocessing import StandardScaler

🔹 2. Criando um Conjunto de Dados

Para este exemplo, vamos criar um conjunto de dados sintético com duas variáveis para facilitar a visualização dos clusters.

# Gerando dados sintéticos
np.random.seed(42)

# Criando dois clusters distintos
cluster1 = np.random.normal(loc=[5, 5], scale=1.0, size=(100, 2))
cluster2 = np.random.normal(loc=[10, 10], scale=1.0, size=(100, 2))

# Concatenando os dados
dados = np.vstack((cluster1, cluster2))

# Criando um DataFrame
df = pd.DataFrame(dados, columns=["Feature 1", "Feature 2"])

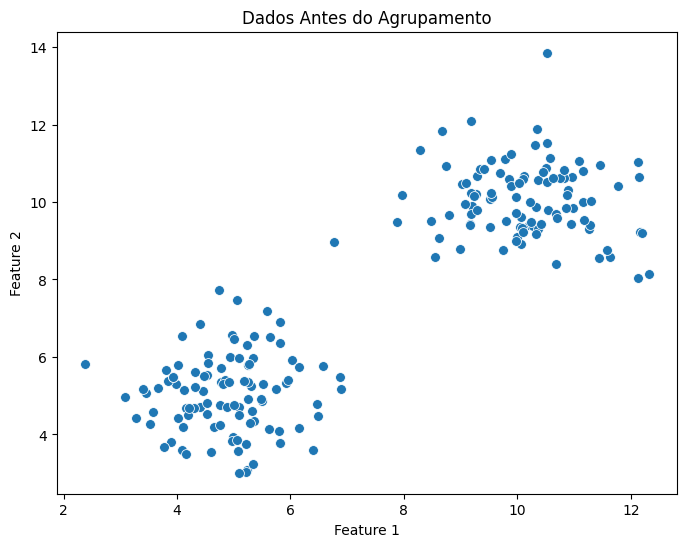
Vamos visualizar os dados brutos antes do agrupamento:

plt.figure(figsize=(8, 6))
sns.scatterplot(x=df["Feature 1"], y=df["Feature 2"], s=50)
plt.title("Dados Antes do Agrupamento")
plt.show()

🔹 3. Normalizando os Dados

O K-Means é sensível à escala das variáveis, então é importante padronizá-las:

scaler = StandardScaler()
df_normalizado = scaler.fit_transform(df)

Agora nossos dados estão prontos para serem clusterizados!

🔹 4. Aplicando o Algoritmo K-Means

Vamos definir o número de clusters e aplicar o K-Means:

kmeans = KMeans(n_clusters=2, random_state=42)
kmeans.fit(df_normalizado)

Depois de treinar o modelo, podemos obter os rótulos dos clusters atribuídos a cada ponto:

df["Cluster"] = kmeans.labels_

🔹 5. Visualizando os Resultados

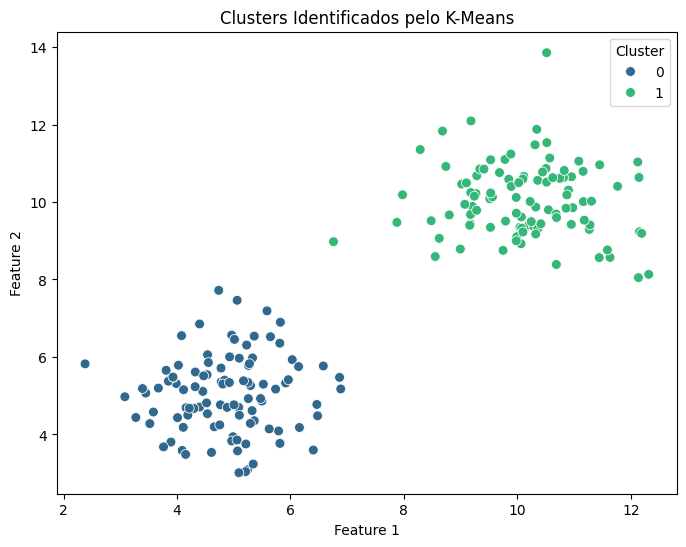
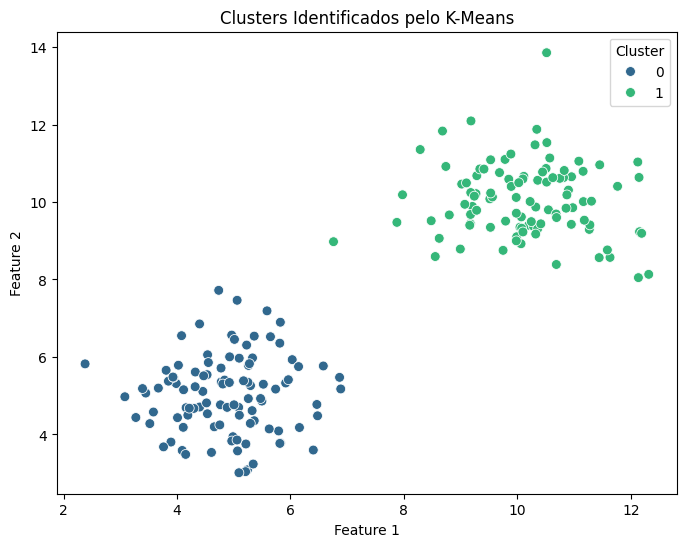
Agora, vamos visualizar os clusters gerados pelo K-Means:

plt.figure(figsize=(8, 6))
sns.scatterplot(x=df["Feature 1"], y=df["Feature 2"], hue=df["Cluster"], palette="viridis", s=50)
plt.title("Clusters Identificados pelo K-Means")
plt.show()

🔹 6. Escolhendo o Número Ótimo de Clusters (Método do Cotovelo)

O método do cotovelo nos ajuda a encontrar o número ideal de clusters. Ele calcula a inércia (soma das distâncias quadradas dos pontos ao centro do cluster) para diferentes valores de k.

inercias = []
k_values = range(1, 10)

for k in k_values:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(df_normalizado)
    inercia = kmeans.inertia_
    inercias.append(inercia)

plt.figure(figsize=(8, 6))
plt.plot(k_values, inercias, marker='o', linestyle='--')
plt.xlabel("Número de Clusters")
plt.ylabel("Inércia")
plt.title("Método do Cotovelo")
plt.show()

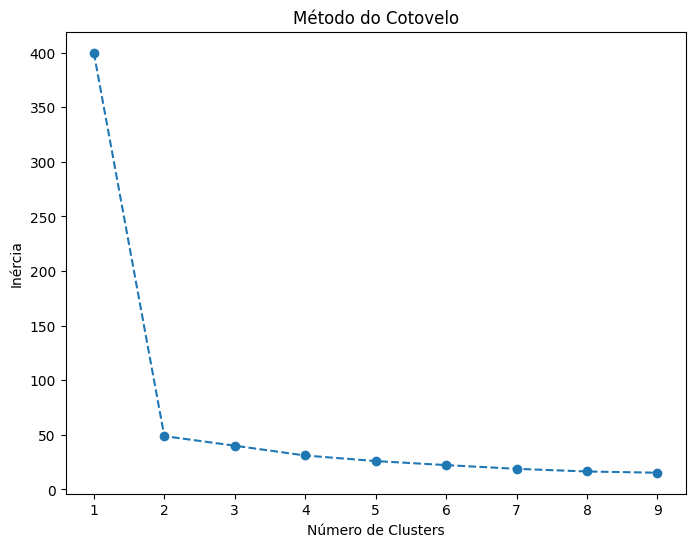
O ponto onde a curva começa a achatar indica o número ideal de clusters.

🎯 Conclusão

O K-Means é uma poderosa técnica de agrupamento que pode ser usada para segmentação de clientes, análise de padrões e muito mais. Neste tutorial, você aprendeu:

✅ Como gerar e visualizar dados;
✅ Como normalizar os dados para o K-Means;
✅ Como aplicar o algoritmo e interpretar os clusters;
✅ Como usar o método do cotovelo para escolher o melhor k.

Agora é sua vez de testar! Experimente com seus próprios dados e veja os resultados. 🚀🔥

Read more